在我发表了关于随机矩阵理论（RMT）的介绍之后，我认为值得探索如何通过它来更好地衡量资产组合。我将首先讨论相关矩阵的实用性，并推导一个类似的随机矩阵。然后利用它的特性，从一些真实的金融相关数据中过滤出随机性，并演示如何利用它来制定更好的投资组合。

相关矩阵及其随机矩阵模拟

现代投资组合理论（MPT）是由哈里?马科维茨（Harry Markowitz）在1952年提出的，它是一种构建金融资产组合的方法，使投资者能够在风险和回报之间进行权衡。给定一组股票，可以计算出一组权重，用于最大化期望风险水平的回报，或最小化所选回报的风险。如果投资组合中的股票在某种宏观经济波动的影响下同时涨跌，那么风险和回报都会增加。例如，对股票持乐观态度而对债券持悲观态度的策略本身就具有风险，因为这两种资产在危机时期往往走向相反的方向。因此，在计算资本最优配置的权重时，相关性显然是一个重要的因素。给定一个相关矩阵和一个期望风险或期望回报，可以计算第三个变量。

那么这和随机矩阵有什么关系呢？最常用的相关矩阵，皮尔森估算器（the Pearson estimator），只是对总体相关矩阵的精确估计，在这种情况下，资产价格点趋于无穷。在现实中，股票价格数据的抽样误差和有限的样本容量都会引入显著的噪声。这意味着样本相关矩阵本质上是随机的。过滤掉一些这种随机性可以改善资本配置，从而增加回报或降低风险。

即使考虑到中等数量的资产N，相关矩阵也会迅速增大。包含N (N?1)/2个唯一项。分析个体相关性的重要性显然是不可行的，这就是随机矩阵发挥作用的地方。相关随机变量的矩阵可以作为一个零假设来评估经验相关矩阵的哪些部分是噪声，哪些是信号。

考虑一个N × M的价格观察矩阵，这样每一行对应一个金融资产。当然，真正相关的并不是资产的绝对价格，而是它们随时间的变化。计算价格变动百分比可以实现这一点，同时也使每一行的单位具有可比性。此外，如果要构造一个具有相似性质的随机矩阵，我们必须了解观测结果来自于什么分布。在最常用的股票价格模型——几何布朗运动下，未来价格变化被认为是对数正态分布。这将在以后使用真实数据加以验证，但目前仅假设是这样就足够了。因此，取百分比乘数(1 +?%)的对数，并将每一行归一化，使其均值为零，方差为1是合乎逻辑的。

由于数据经过了归一化处理，样本相关矩阵就等于样本协方差矩阵：

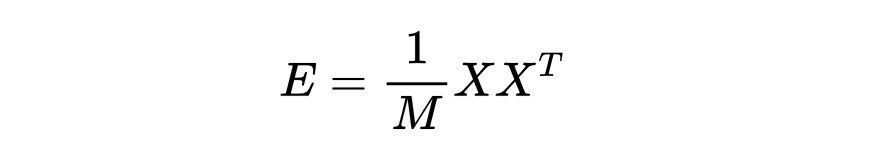
如果价格数据实际上是随机的，那么构造随机矩阵集合就很简单了。我们通过创建一个N × M矩阵H，其中包含从N(0,1)分布中提取的元素，并完成相同的计算，W = (1/M)HH^T。将数据限制在 M > N，从这个过程中产生的所有矩阵的集合就是Wishart-Laguerre集合。该集合最早由John Wishart于1928年使用，长期以来一直用于多元数据分析。与著名的高斯系综相似，它被定义为三维系综。这里只使用实际情况，因此将其称为WL集合。

Wishart-Laguerre集合的性质

可以很容易地证明WL矩阵是厄米特矩阵。从我们对GOE的早期研究可以得出，它们有N个正特征值。其次，考虑WL集合特征值的分布；将它们绘制为2000×2000 WL矩阵将生成众所周知的Mar?enko-Pastur分布（图1）。

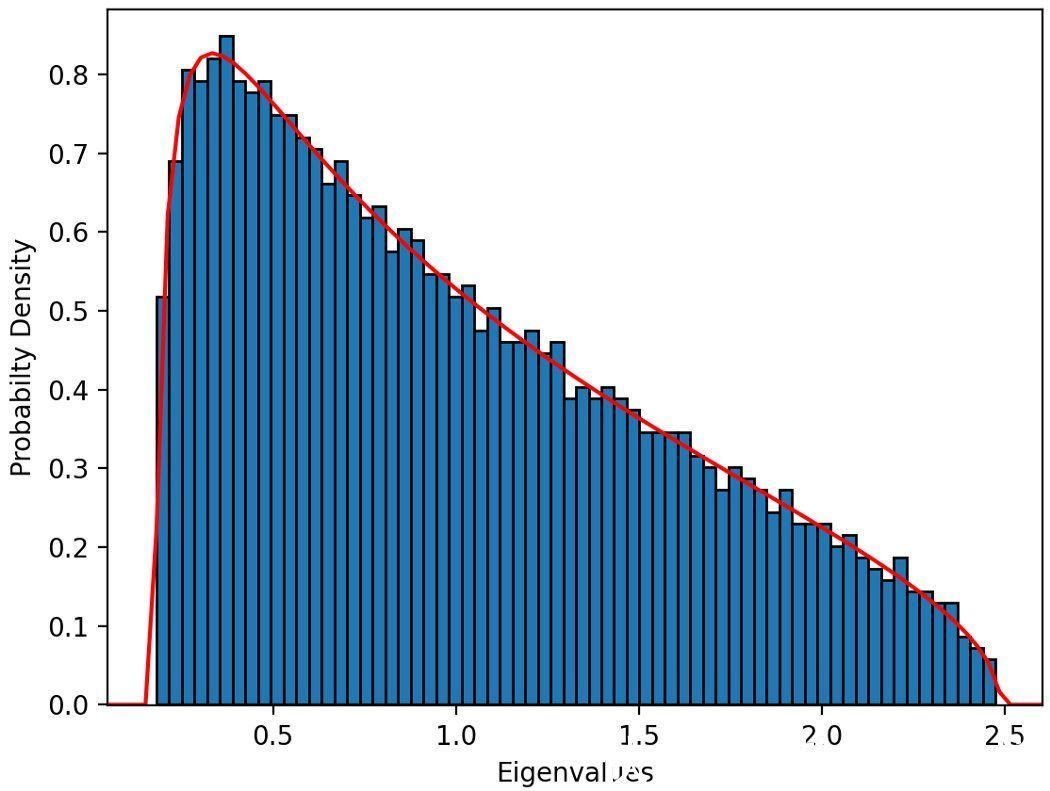
• 图1：一个2000x2000的WL矩阵的Mar?enko-Pastur分布

极限分布（红色）具有密度：

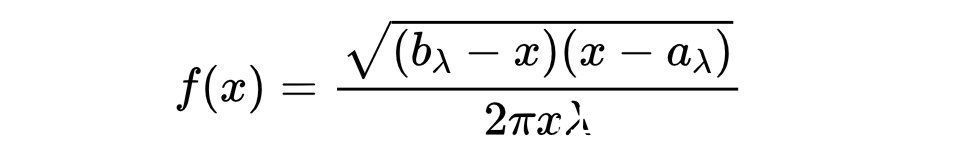
式中，aλ和bλ为矩形比λ = N/M∈(0,1)的函数，计算公式为aλ =(1?λ)^2，bλ =(1+ λ)^2。这些值也是特征值的最大值和最小值，在特征值之外f(x) = 0。在图1中，使用M = 6000的值，得到λ = 1/3的矩形比。

图2中可以看出特征值密度如何依赖于λ，以及如果M≤N，Mar?enko-Pastur分布如何失效。

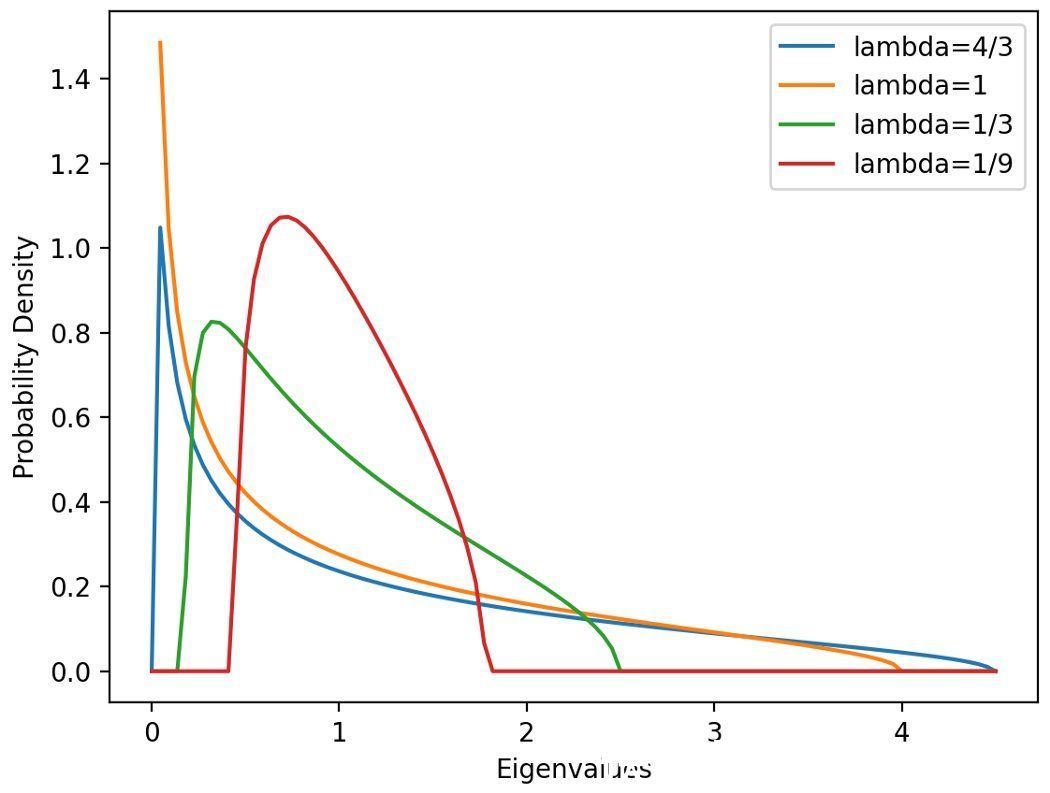
• 图2：Mar?enko-Pastur不同矩形比的分布。值得注意的是，在一般情况下，分布还取决于数据的方差。但是，当我们处理简化的数据时，为了简洁起见，我们省略了这一点。

在λ→0的极限下，显然λ = bλ = 1。这对应于资产数N固定，观测数M→∞的情况。数据中的噪声量降为零，我们能够很好地测量相关矩阵。

实证金融数据的性质

在本节中，我们将真实股票市场数据的行为与WL集合的行为进行比较，以研究一种过滤方法，从而改进相关矩阵。我们讨论的数据集是2016-2020年5年间在纽约证券交易所上市的所有美国大型公司的股价，有效股票为508个，每个股票选取1259个价格。这些被排列成一个508 × 1258的矩阵P，这样，第i行对应于股票i的每日百分比价格变化（应用对数后）。

文章来源：《金融理论探索》 网址: http://www.jrllts.cn/zonghexinwen/2022/0424/533.html