首先，前面的价格变化是对数正态分布的假设，可以用一种新的方法来检查。P的每一行都被独立地洗牌以消除任何时间依赖性。如果被打乱的行遵循N(0,1)分布，则相关矩阵预期遵循Mar?enko-Pastur分布。计算E = 1/1258 PP^T并绘制E的特征值密度，证实了每日价格变化实际上是对数正态分布（图3）。

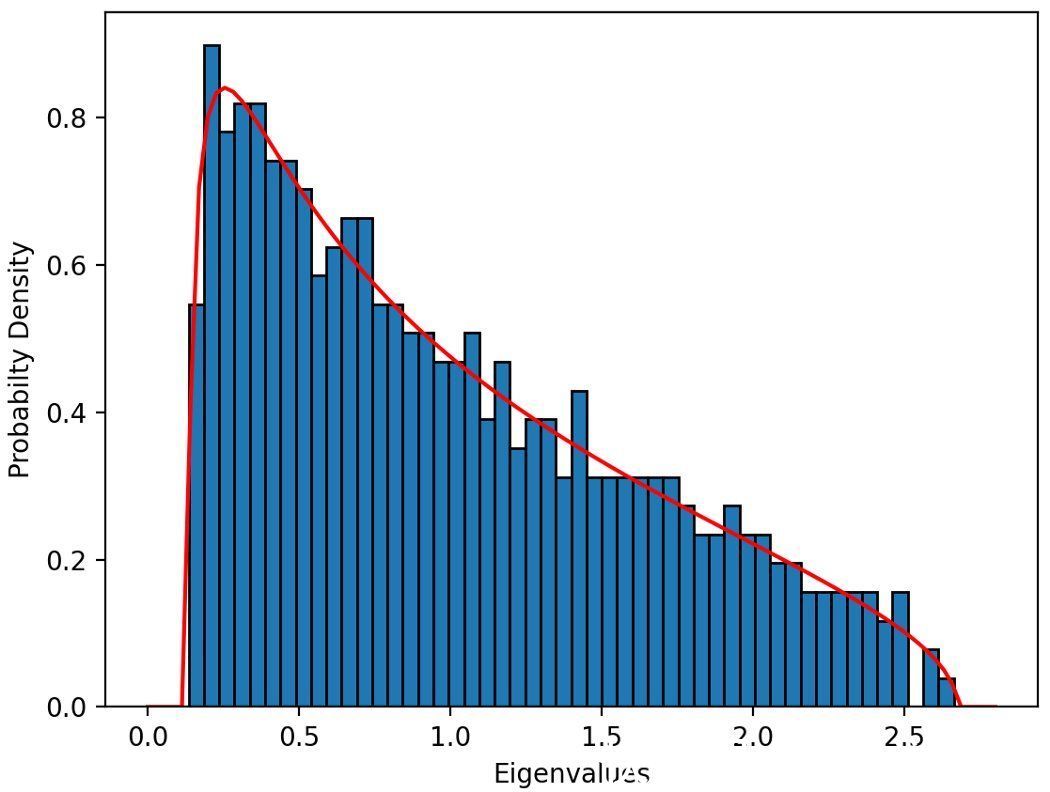
• 图3：当=508/1258=0.404时，理论分布（红色）为mar?enko-Pastur密度

由此可以得出，当数据没有被打乱时，任何偏离Mar?enko-Pastur分布的情况都表明存在某种底层结构。在股市数据中完全可以预料到这种情况，否则价格变化将是完全随机的。图4显示了原始数据（未经过洗牌）的相关矩阵特征值的分布。有一些较大的特征值被裁剪出图中，其中最大的约为207。这被称为市场模式，因为它代表了整个市场的价格联动。

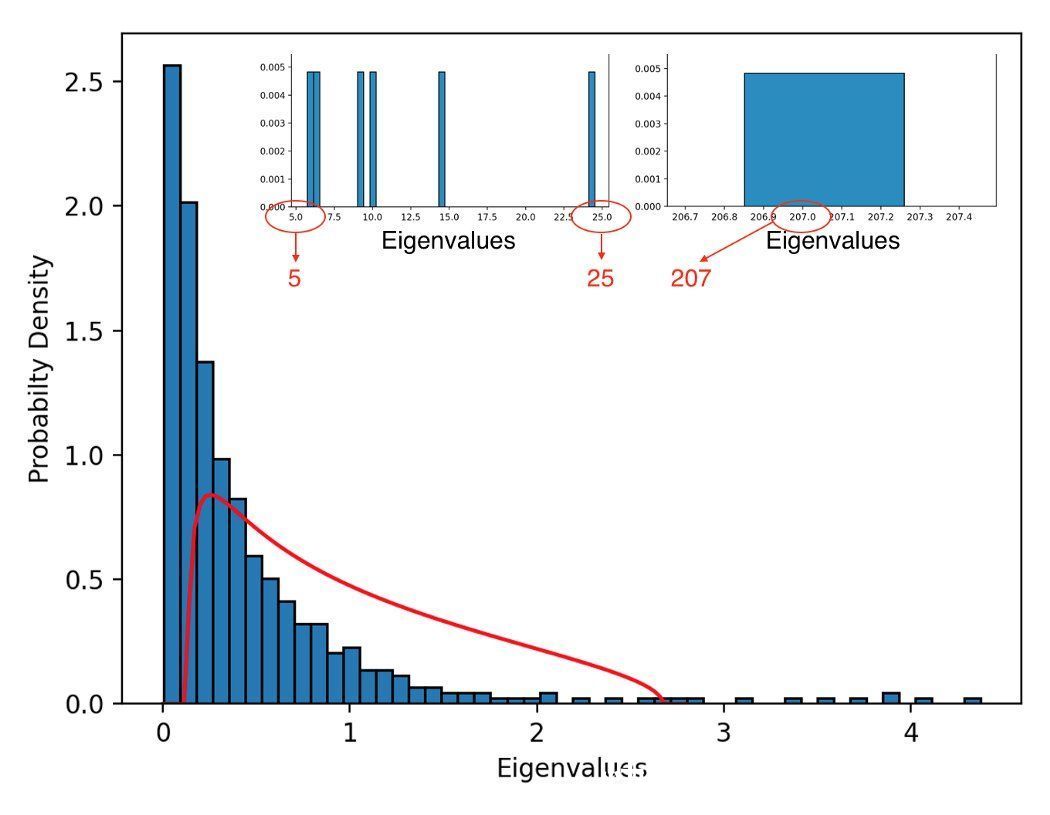
• 图4：原始股市数据相关矩阵的特征值密度。如图3所示，=0.404的Mar?enko-Pastur密度用红色覆盖。

最初，我们可能会担心如此大量的特征值落在Mar?enko-Pastur密度给出的最小值以下，这似乎是一个非常糟糕的拟合。然而，这是意料之中的。aλ和bλ之间的特征值被判定为数据中随机的产物，因此被忽略，或从特征值集合中“过滤”出来。

低于理论最小值的特征值也被忽略。每个特征值对应一个比例方差的投资组合，所以一个小的特征值意味着存在一个可以在几乎为零的风险下提供非零回报的权重。这被认为是不合理的。现在我们把注意力转向这些特征值被“过滤掉”的数学过程。

一种测试相关滤波有效性的方法

评估相关矩阵滤波有效性的最好方法是衡量一个真实的投资组合的收益，在看不见的数据上进行测试，当投资组合的权重分别使用原始的相关矩阵和过滤后的相关矩阵计算时。但自上世纪70年代以来，人们普遍认为，投资组合的最佳规模是大约30只股票。由于股票选择并不是本文的重点，所以我们随机选择了30支股票。

数据被分成两半。前629个价格变化被指定为“训练”数据，用于构建最优投资组合权重集。剩下的629个价格将被用来测试过滤的有效性。

过滤相关矩阵的过程涉及到将不需要的特征值从集合中替换出来。这可以用许多不同的方法来完成，这里使用的方法是用所有过滤特征值的平均值来替换每一个。这具有保持相关矩阵轨迹的效果。由这组特征值重建相关矩阵很简单，因为它是实数和对称的，可以使用特征分解定理的一个特殊情况：

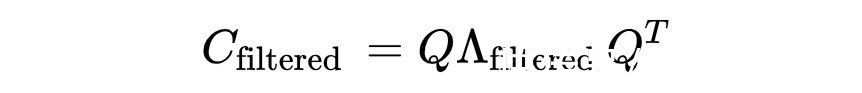
其中Q是列为C的特征向量的矩阵，Λ_filtered是包含新特征值集合的对角矩阵。一旦重建，C_filtered的对角元素必须设为1，以保持相关性矩阵的直观概念。

现代投资组合理论的核心原则是，它允许投资者根据自己的个人偏好在风险和回报之间进行权衡。由于选择期望回报的概念比选择风险更直观，因此在构建一个最优投资组合以最小化给定回报的风险时，这是惯例。然而，为简单起见这里构建的投资组合将具有最小的方差（风险），无论回报如何。目的是在使用过滤后的相关矩阵时获得更大的收益。计算方差最小的权值集合w相当于求解矩阵形式的线性规划问题，其解可导出为：

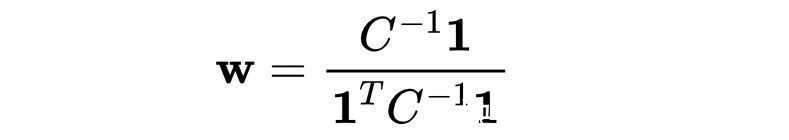
值得注意的是，最优的权值集可能包含负值。在金融术语中，这些对应于做空。为简单起见，通过将负权值设置为零并重新规范化其余的权值，消除了这种可能性。因为散户投资者通常只会购买股票，而不会“做空”股票。我们现在可以检验相关矩阵滤波的有效性。

结果与不足

按照上面列出的方法，w中的每个最小方差权重平均变化1.1%。在629天的测试期内，使用原始投资组合的最终累积收益率为48.6%，但使用相关矩阵滤波（图5）时，该收益率上升到58.9%。虽然简单，但这说明了随机矩阵理论提高投资组合绩效的潜力。

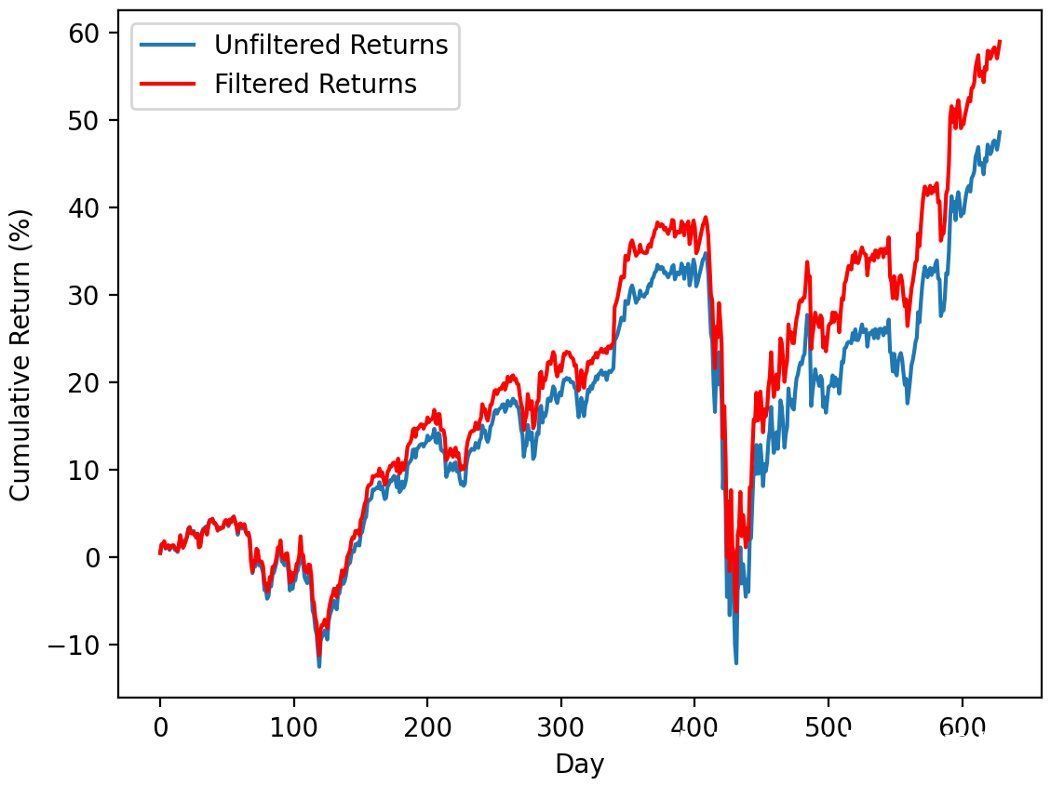
• 图5：使用未过滤和过滤相关矩阵时的629天测试期间的累计收益

这里概述的方法的主要不足是，只有一个随机选择的股票被测试。理想情况下，给定必要的时间和计算能力，将使用自助方法。这将包括测试许多不同的随机组合，并对结果进行平均。

结论

皮尔森相关矩阵的一个随机类比已经导出，研究了其特征值的分布，得到了Mar?enko-Pastur分布。然后，这被用来确定实际相关矩阵的哪些部分由于随机性而发生。然后计算出更好的投资组合权重，并对结果进行比较。

文章来源：《金融理论探索》 网址: http://www.jrllts.cn/zonghexinwen/2022/0424/533.html